იპოვეთ მერხევი სხეულის მაქსიმალური სიჩქარე თუ ამპლიტუდა 8 სმ-ია პერიოდი კი 6 წმ.

მოცემულია რომ \(A=8\) სმ=\(8\cdot 10^{-2}\) მ და \(T=6\) წმ. უნდა ვიპოვოთ \(v_{max}\).

გთავაზობთ ამოხსნის ორ გზას:  I გზა შეგიძლიათ გამოიყენოთ როგორც მათემატიკური ასევე ზამბარიანი ქანქარის დროსაც, ხოლო II გზაში ჩვენ განვიხილავთ მათემატიკური ქანქარის შემთხვევას, ზამბარიანი ქანქარის დროსაც ანალოგიურად იქნება.

I გზა:  როგრც ცნობილია რხევის დროს სხეულის კოორდინატი გამოითვლება შემდეგი ფორმულით \(x=A\cos(\omega t)\) სადაც \(\omega\) ციკლური სიხშირეა და ტოლია \(\omega=\frac{2\pi}{T}\), სხეულის სიჩქარე ტოლია მანძილის პირველი რიგის წარმოებულის, ანუ \(v={x}'=A\omega\sin(\omega t)\), ამ ფორმულიდან გამომდინარეობს რომ \(v\) მაქსიმალური იქნება მაშინ როდესაც სინუსი იქნება მაქსიმალური, სინუსის მაქსიმალური მნიშვნელობა 1-ია, ესე იგი \(v_{max}=A\omega=A\frac{2\pi}{T}\), რიცხვითი მნიშვნელობების ჩასმით მიიღებთ: \(v_{max}\approx0,08\)მ/წმ.

II გზა: სხეულს მაქსიმალური სიჩქარე ექნება როდესაც ის გაივლის წონასწორობის წერტილში, რადგან ამ დროს მისი პოტენციური ენერგია მინიმალურია, ანუ კინეტიკური მაქსიმალურია (იხილეთ ნახაზი):

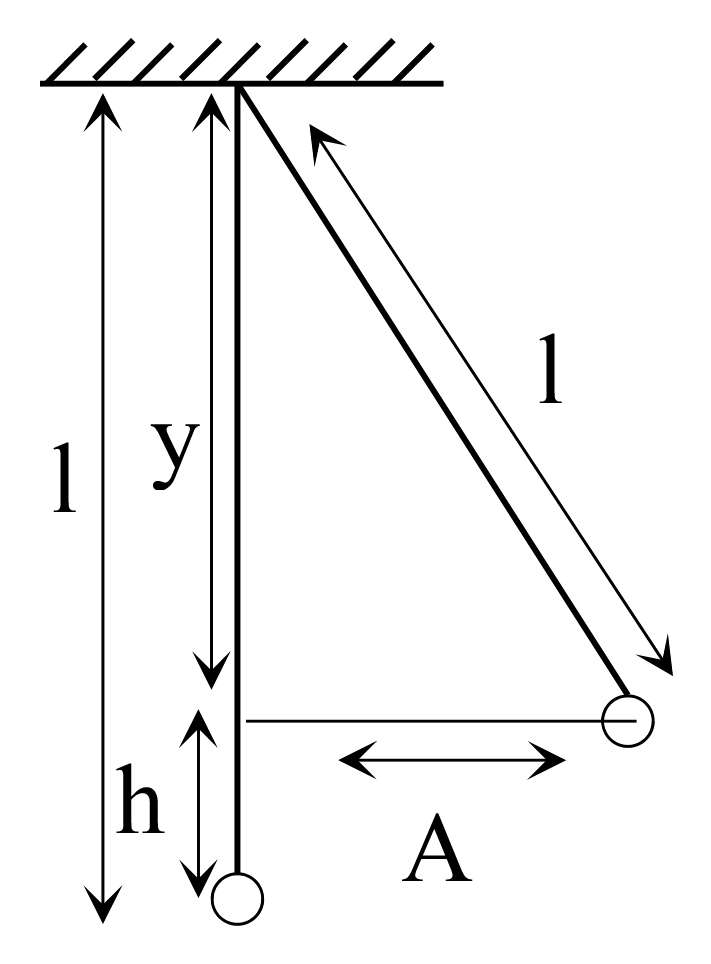\(h\)  სიმაღლეზე სხეულს გააჩნდა პოტენციური ენერგია \(mgh\), წონასწორობის წერტილში ეს ენერგია გადავა კინეტიკურ ენერგიაში \(\frac{mv^{2}}{2}\), ანუ \(mgh=\frac{mv_{max}^{2}}{2}\Rightarrow v_{max}=\sqrt{2gh}\), ამ ფორმულაში ყველაფერი ცნობილია გარდა \(h\)-ისა. ჯერ ვიპოვოთ ქანქარის სიგრძე, როგორც ვიცით \(T=2\pi\sqrt{\frac{l}{g}}\Rightarrow l=\frac{T^{2}g}{4\pi^{2}}\). რიცხვების ჩასმით მივიღებთ რომ \(l\approx 4\)მ. ნახაზის მიხედვით შეგვიძლია დავწეროთ რომ \(y=\sqrt{l^{2}-A^{2}}\), როგორც ნახაზიდან ვხედავთ \(h=l-y\), ყველა ამ ზემოთქმულის გათვალისწინებით გამოთვლით \(v_{max}\) და მიიღებთ რომ იგი დაახლოებით ტოლია 0,08