ელექტრონი, რომელიც v სიჩქარით შეფრინდა B ინდუქციის მაგნიტურ ველში ძალწირების მართობულად, მოძრაობს R რადიუსის წრეწირზე. რა რადიუსის წრეწირზე მოძრაობს ელექტრონი, რომელიც v/2 სიჩქარით შეფრინდა 2B ინდუქციის მაგნიტურ ველში ძალწირების მართობულად?

ამონარიდი  თეორიიდან:

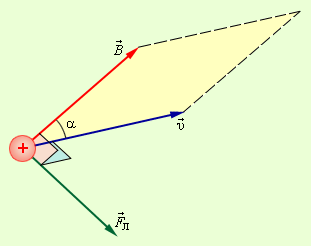
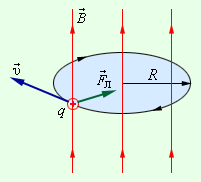
\(F\)ლ\(=qvB\sin \alpha\).

 ამ ძალას ლორენცის ძალას უწიდებენ.  ამ გამოსახულებაში \(\alpha\) კუთხე  \(\vec{v}\) სიჩქარესა და \(\vec{B}\) მაგნიტული ინდუქციის ვექტორს შორის კუთხის ტოლია. დადებითად დამუხტულ ნაწილაკზე მომქმედი ლორენცის ძალის მიმართულება, ამპერის ძალის მიმართულების მსგავსად შეიძლება მარცხენა ხელის ან ბურღის წესის საშუალებით დადგინდეს. \(\vec{F}\)ლ, \(\vec{B}\) და  \(\vec{v}\) ვექრორების ურთიერთ განლაგება დადებითად დამუხტული ნაწილაკისთვის ნახ. 1-ზეა ნაჩვენები.

ნახ. 1.

\(\vec{F}\)ლ, \(\vec{B}\) და  \(\vec{v}\)  ვექრორების ურთიერთ განლაგება. ლორენცის \(\vec{F}\)ლ ძალა რიცხობრივად  \(\vec{v}\) და \(\vec{B}\) ვექტორებზე აგებული პარალელოგრამის ფართობის q მუხტზე ნამრავლის ტოლია

ლორენცის ძალა   \(\vec{v}\) და \(\vec{B}\) ვექტორების მართობულია. დამუხტული ნაწილაკის მაგნიტურ ველში მოძრაობისას ლორენცის ძალა მუშაობას არ ასრულებს. ამიტომ ნაწილაკის მოძრაობისას  ნაწილაკის სიჩქარის სიდიდე არ იცვლება.

თუ დამუხტული ნაწილაკი ლორემცის ძალის მოქმედებით ერთგვაროვან მაგნიტურ ველში მოძრაობს, ხოლო მისი \(\vec{v}\) სიჩქარე \(\vec{B}\) ვექტორის მართობულ სიბრტყეში მდებარეობს, მაშინ ნაწილაკები იმოძრავებენ წრეწირზე ცენტრისკენული აჩქარებით  $$\(\frac{v^{2}}{R}\)     და ამის მიზეზია

ლორენცის ძალა. ნიუტონის მეორე კანონის თანახმად   \(qvB=m\)\(\frac{v^{2}}{R}\) . აქედან კი ბრუნვის რადიუსი  

 \(R=\frac{mv}{qB}\)

ამ შემთხვევაში ლორენცის ძალა ცენტრისკენული ძალის როლს ასრულებს (ნახ. 2).

ნახ. 2.

დამუხტული ნაწილაკის წრიული მოძრაობა ერთგავროვან მაგნიტურ ველში

ერთგავროვან მაგნიტურ ველში ნაწილაკის ბრუნვის პერიოდი ტოლია

 \(T=\frac{2\pi R}{v}=\frac{2\pi m}{qB}\).

ეს გამოსახულება უჩვენებს, რომ მოცემული მასის დამუხტული ნაწილაკების ბრუნვის პერიოდე არ არის დამოკიდრბული \(v\) სიჩქარესა და ტრაექტორიის R რადიუსზე.

წრიულ ტრაექტორიაზე დამუხტული ნაწილაკების მოძრაობის კუთხურ სიჩქარეს

 \(\omega =\frac{v}{R}=v\frac{qB}{mv}=\frac{qB}{m}\)

ციკლოტრონულ სიჩქარეს უწოდებენ. ციკლოტრონული სიჩქარე არ არის დამოკიდებული ნაწილაკის სიჩქარეზე (და ე.ი. არც კინეტიკურ ენერგიაზე).