$\gamma =\frac{c_{p}}{c_{v}}=\frac{c_{v}+R}{c_{v}}=1+\frac{R}{c_{v}}$      (1)

ნარევის შინაგანი ენერგია $U=U_{1}+U_{2}=\nu _{1}\frac{RT}{\gamma _{1}-1}+\nu _{2}\frac{RT}{\gamma _{2}-1}$         (2)

მეორესმხრივ $U=\nu c_{v}T=\left ( \nu _{1}+ \nu _{1}\right )c_{v}T$              (3)

(2) და (3) =>

$c_{v}=\frac{\nu _{1}R\left (\gamma _{2}-1 \right )+\nu _{2}R\left (\gamma _{1}-1 \right )}{\nu _{1}\left (\gamma _{2}-1 \right )+\nu _{2}\left (\gamma _{1}-1 \right )}$        (4)

ჩავსვათ (4) გამოსახულება (1)-ში, მივირებთ:

$\gamma =\frac{\nu _{1}\gamma _{1}\left ( \gamma _{2}-1 \right )+\nu _{2}\gamma _{2}\left ( \gamma _{1}-1 \right )}{\nu _{1}\left ( \gamma _{2}-1 \right )+\nu _{2}\left ( \gamma _{12}-1 \right )}$

ვიციტ წნევის სიმაღლის მიხედვიტ განაწილების ბარომეტრული კანონი (12.6), სადაც თუ ჩავთვლისთ, რომ ზღვის დონის სიმაღლე არის ნული, მაშინ (12.6) ასე ჩაიწერება

$P=P_{0}e^{-\frac{mgh}{RT}}$

სიმაღლის შესაბამისი მნიშვნელობების ჩასმით (ერთ შემთხვევაში 5კმ და მეორე შემთხვევაში -5კმ) მივიღებთ სასუღველ შედეგს იმის გათვალისწინებით, რომ დედამიწის ზედაპირზე ნორმალურ პირობებში წნევა არის 1 ატმოსფერო.

h სიმაღლეზე განვიხილოთ dh სისქის თხელი ფენა. ამ ფენაზე ქვევიდან მოქმედებს p წნევა, ხოლო ზევიდან p+dp წნევა. ფენის მასა არის $Sdh\rho$, სადაც S არის ფენის რადიუსი. დავწეროთ ფენაზე მოქმედი ძალების ტოლობა

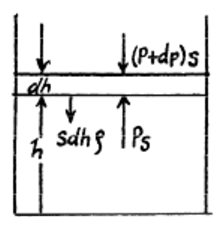
$Sdh\rho g+\left ( p+dp \right )S=pS$, აქედან გვექნება,

$dp=-\rho gdh$. 

აირის მდგომარეობის განტოლებიდან ვიცით,

$p=\frac{\rho }{M}RT$, ამიტომ მუდმივი ტემპერატურის დროს  $dp=\frac{d\rho }{M}RT$

ასე რომ   $\frac{d\rho }{\rho }=\frac{gM}{RT}dh$

შესაბამის საზღვრებში გაინტეგრებით

$\int_{\rho _{0}}^{\rho }\frac{d\rho }{\rho }=\int_{0}^{h}\frac{gM}{RT}dh$

ანუ

$ln\frac{\rho _{0}}{\rho }=-\frac{gM}{RT}h$

ასე რომ, $\rho =\rho _{0}e^{-Mgh/RT}$ და $h=-\frac{RT}{Mg}ln\frac{\rho }{\rho _{0}}$

(ბ) მოცემულია $T=273^{o}K$,  $\frac{\rho _{0}-\rho }{\rho_{0} }=0,01$ ანუ   $\frac{\rho }{\rho_{0} }=0,99$

ამიტომ    $h=-\frac{RT}{Mg}ln\frac{\rho }{\rho _{0}}$=0,09კმ