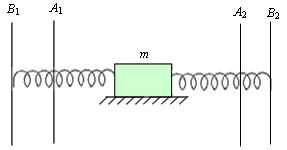
ma = -(k1+k2)x,
ანუ
.\(a+\frac{k_{1}+k_{2}}{m}x=0\)
ამ განტოლებაში \(\omega _{0}=\sqrt{\frac{k_{1}+k_{2}}{m}}\) - არის ტვირთის რხევის საკუთარი სიხშირე. როგორც ჩანს, ის არ არის დამოკიდებული ტვირთის წანაცვლებაზე. რხევის პერიოდი დაკავშირებულია საკუთარ სიხშირესთან ასე \(T=\frac{2\pi }{\omega _{0}}\) . შესაბამისად, არც პერიოდი არ არის დამოკიდებული ტვირთის წანაცვლებაზე.
პასუხი: რხევის პერიოდი არ იცვლება.
\(F_{re}=\frac{\mathrm{d} \left (mv \right )}{\mathrm{d} t}\)
რადგან \(v=const\)
\(F_{re}=v\frac{\mathrm{d} m}{\mathrm{d} t}\)
რადგან \(m=\rho V\), სადაც \(\rho\) არის წყლის სიმკვრივე და მუდმივია, ხოლო \(V=Svt\), ამიტომ
\(F_{re}=S\rho v^{2}\) (1)
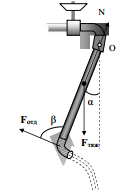
მინის მილზე მოქმედებს მის სიმძიმის ცენტრში მოდებული სიმძიმის ძალა, რომელიც შედგება თვითონ მილის სიმძიმის ძალისა და მასში მყოფი წყლის სიმძიმის ძალების ჯამისგან
\(F_{g}=(m_{T}+Sl\rho )g\) (2)
გადახრილი მილის წონასწორობა მოითხოვს, რომ სიმძიმის ძალისა და უკუცემის ძალების მომენტების ჯამი იყოს ნული:
\(M_{g}+M_{re}=0\) (3)
სიმძიმის ძალის მომენტი О ღერძის მიმართულების გათვალისწინებით:
\(M_{g}=-\frac{1}{2}F_{g}l\sin \alpha\) (4)
აქ \(\frac{1}{2}l\sin \alpha\) არის О ღერძის მიმართ სიმძიმის ძალის მხარი.
უკუცემის ძალის მომენტი იქნება
\(M_{re}=F_{re}l\) (5)
ჩავსვათ (4) და (5) გამოსახულება (3)-ში:
\(F_{re}l=\frac{1}{2}F_{g}l\sin \alpha\) (6)
ახლა ჩავსვათ (1) და (2) ბოლო (6) გამოსახულებაში და საბოლოოდ მივიღებთ:
\(\sin \alpha =\frac{2S\rho v^{2}}{\left ( m_{T}+Sl\rho \right )g}\).
ბორბლის გარსის ნებისმიერი წერტილი, მაგალითად В მონაწილეობს ორ მოძრაობაში - გადატანითში სიჩქარით 
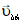
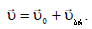
В წერტილის მდებარეობა t მომენტში განისაზღვრება 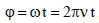
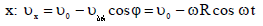
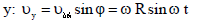
სიჩქარის მოდული 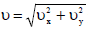
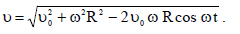
განსაზღვრების თანახმად 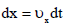
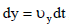
x(0) = 0, y(0) = 0 მივიღებთ:
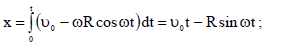
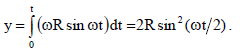
მაშინ А შეეხება გზის ზედაპირს დროის იმ მომენტში, როცა у=0. განტოლებიდან (6), გამოდის:

სადაც n = 1,2,3,…….. დროის ამ მომენტებში, (2)-სა და (3)-ის თანახმად სიჩქარეები შესაბამისად იქნება:
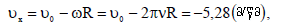
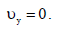
რადგან 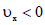
პასუხი: 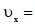
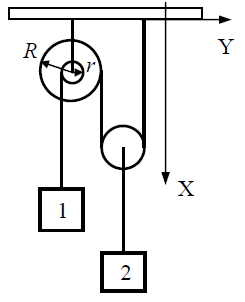
ვთვლით 1 და 2 სხეულებს მატერიალურ წერტილებად, ძავფს კი უჭიმვადად. ძაფები ჭოჭონაქების მიმართ არ სრიალებენ.
II. ვთქვათ დროის მცირე Δt ინტერვალში პირველი სხეულის კოორდინატის ცვლილება არის Δx1 (სიცხადისთვის ვთქვათ იგი ეშვება). რადგან ძაფი უჭიმვადია, ამიტომ r რადიუსის ცილინდრის შემობრუნების \(\Delta \varphi\) კუთხე უკავშირდება Δx1-ს ასე
\(\Delta x_{1}=r\Delta \varphi\) (1)
ამასთან R რადიუსის ცილინდრი შემობრუნდება ამავე კუთხით, ხოლო ძაფის სიგრძე, რომელიც მასზეა მოთავსებული და რომელზეც ჰკიდია სხეული 2 შეიცვლება სიდიდით:
\(\Delta l=-R\Delta \varphi\) (2)
მეორე ჭოჭონაქის ცენტრის და ესეიგი მეორე სხეულის კოორდინატის ცვლილება იქნება:
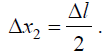
III. განტოლებათა (1) – (3) სისტემის ამოხსნა გვაძლევს ორი სხეულის კოორდინატთა ცვლილებებს შორის კავშირის განტოლებას:
\(\Delta x_{2}=-\frac{R}{r}\frac{\Delta x_{1}}{2}\) (4)
ამ განტოლების მარჯვენა და მარცხენა მხარეები გავყოთ დროის მცირე შუალედზე და \(\Delta t\rightarrow 0\) ზღვარზ ე გადასვლით მივღებთ სხეულების სიჩქარეებს შორის კავშირის განტოლებას:
\(v_{2}=-\frac{R}{r}\frac{v_{1}}{2}\) (5)
მიღებული თანაფარდობის დროით გაწარმოებით მივიღებთ სხეულების აჩქარებებს შორის კავშირს:
\(a_{2}=-\frac{R}{r}\frac{a_{1}}{2}\) (6)