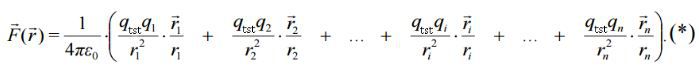უნდა აღინიშნოს, რომ ელექტროსტატიკური ურთიერთქმედების კანონის ფორმულირება მოიცემა „წერტილოვანი“ სხეულებისთვის. ცდა აჩვენებს, რომ ელექტროსტატიკური ურთიერთქმედების ძალებისთვის სამართლიანია სუპერპოზიციის პრინციპი. ყოველი ელექტრული ზემოქმედება წერტილოვან მუხტზე (დავარქვათ მას საცდელი მუხტი) მუხტების ჯგუფიდან თითოეული მუხტის მხრიდან აღიწერება ძალით - ვექტორული სიდიდით, რომელიც შეიძლება მოიძებნოს კულონის კანონით. მთელი n მუხტისგან შედგენილი ჯგუფის ელექტრული ზემოქმედება ყველა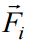 
ძალის ვექტორული ჯამის ტოლია
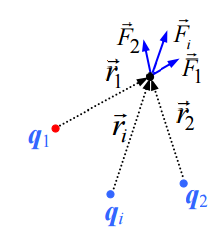
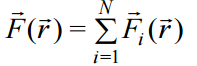(15.2)
ეს ელექტროსტატიკური ძალების მნიშვნელოვანი თვისება არის. ორი მუხტის ურთიერთქმედების ძალა არ იცვლება მესამე, მეოთხე და ა.შ. მუხტების არსებობით.
ახლა ელექტრული ველის, როგორც სხეულების ელექტრულ ურთიერთქმედებაში შუამავლის კონცეფციაზე დაყრდნობით შემოვიტანოთ ელექტრული ველის მნიშვნელოვანი მახასიათებელი - ელექტრული ველის დაძაბულობა.
ელექტრული ველის დაძაბულობა ეწოდება ველის მოცემულ წერტილში მოთავსებულ საცდელ (წერტილოვან) მუხტზე მოქმედი ძალის ფარდობას ამ საცდელი მუხტის სიდიდესთან.
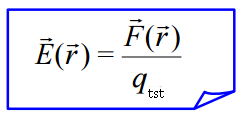(15.3)
აქ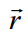 
არის ათვლის მოცემულ სისტემაში წერტილის მდებარეობის მახასიათებელი რადიუს-ვექტორი.
ახლა ავხსნათ, თუ რატომ დაგვჭირდა საცდელი მუხტის სიდიდეზე გაყოფა. წარმოვიდგინოთ, რომ საცდელი მუხტი მოთავსებულია სხვა წერტილოვანი მუხტების ველში. მასზე კულონის კანონით და სუპერპოზიციის პრინციპის გათვალისწინებით მოქმედებს ძალა
ჩანს, რომ სისტემის ყველა შესაკრებს აქვს თანამამრავლი \(\dpi{120} q_{tst}\). ამიტომ ტოლქმედი ძალა პროპორციულია \(\dpi{120} q_{tst}\)-ის. ახლა კი ნათელია, რომ ამ ძალის \(\dpi{120} q_{tst}\)-ზე გაყოფით მივიღებთ სიდიდეს, რომელიც არ არის საცდელი მუხტის სიდიდეზე (და საერთოდ მის არსებობაზე) დამოკიდებული ანუ ახასიათებს თვით მუხტების სისტემის ძალების ველს. სწორედ ეს არის დაძაბულობა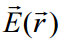 
.
ასე რომ, ფუნქცია 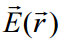ახასიათებს სივრცის ყოველ წერტილს. თუ მოცემულია ასეთი ფუნქცია 
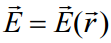, ამბობენ, რომ „მოცემულია ველი“. არსებითად, სწორედ ვექტორული ფუნქცია 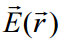არის ელექტრულ ველი. რატომ არის ასეთი მახასიათებლის შემოღება მოსახერხებელი? თუ რამენაირად ვისწავლით მუხტების მოცემული განაწილებით (თეორიულად ან ექსპერიმენტულად) ვიპოვოთ ელექტრული ველის დამოკიდებულებას კოორდინატზე - 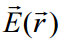, შევძლებთ ვიპოვოთ ძალა, რომელიც მოქმედებს ნებისმიერ საცდელ q მუხტზე, რომელიც მოთავსებულია მოცემულ წერტილში:
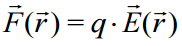(15.4)
წერტილოვანი მუხტის ველის დაძაბულობა
კულონის კანონიდან და ელექტრული ველის დაძაბულობის განსაზღვრებიდან მარტივად მიიღება ერთეულოვანი მუხტის ელექტრული ველის დაძაბულობა
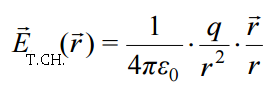. (15.5)
გადავწეროთ (*) ტოლობა ასე:
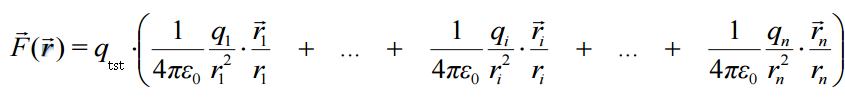
ანუ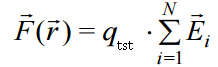 
,
მაშინ (15.4)-ის გათვალისწინებით შედეგად მივიღებთ ელექტრული ველის დაძაბულობის სუპერპოზიციის პრინციპს.
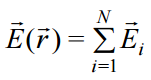
იმისათვის, რათა მივიღოთ განფენილი დამუხტული სხეულის ელექტრული ველის დაძაბულობა, აუცილებელია დავყოთ ის მცირე ელემენტებად (წერტილოვანი მუხტებად), ხოლო შემდეგ გამოვიყენოთ სუპერპოზიციის პრინციპი. მაგალითად ასეთი მეთოდით შეიძლება ვიპოვოთ დამუხტული სფეროს ელექტრული ველის დაძაბულობა. სფეროს გარეთ მისი ელექტრული ველის დაძაბულობა ისეთივეა, როგორც წერტილოვანი მუხტისა, რომელიც მოთავსებულია სფეროს ცენტრში, ხოლო სფეროს შიგნით დაძაბულობა ნულის ტოლია.
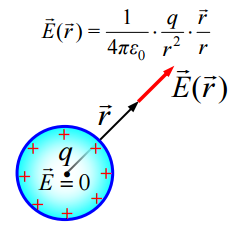
მიუხედავად მარტივი გეომეტრიისა ამის დამტკიცება საკმაოდ ჩახლართული მათემატიკური ამოცანაა და მოგვიანებით ვაჩვენებთ, თუ როგორ შეიძლება გაუსის ინტეგრალური თეორემის გამოყენებით გაცილებით იოლად დავასაბუთოთ ეს.
♦აქვე რამდენიმე შენიშვნა.
1, საცდელი მუხტი უნდა იყოს წერტილოვანი, ანუ დამუხტული სხეულის გეომეტრიული ზომები უნდა იყოს მცირე. მაგრამ რასთან შედარებით. სამწუხაროდ ამის დადგენა მხოლოდ ექსპერიმენტულად არის შესაძლებელი. საცდელი მუხტის ზომების შემცირებით შედეგი არ უნდა იყოს დამოკიდებული მისი ზომების შემდგომ შემცირებაზე.
2, საცდელი მუხტი სიდიდით უნდა იყოს მცირე. რა არის ამ სიმცირის კრიტერიუმი? ელექტრული ველის დაძაბულობის გასაზომად საცდელი ელექტრული მუხტის გაჩენამ არ უნდა შეცვალოს ამ ველის შემქმნელი მუხტების განაწილება. საკითხი აქაც უფრო ხშირად წყდება ექსპერიმენტულად.