ეინშტეინის ფარდობითობის თეორიის პოსტულატებიდან გამომდინარე შეიძლება მოინახოს კანონები, რომლებიც ერთმანეთს აკავშირებს ერთმანეთისადმი წრფივად და თანაბრად მოძრავი ორი ათვლის სისტემის სივრცულ კოორდინატებსა და დროს. 

ვთქვათ х, у, z, t და  х’, у’, z’ და t’, არის კოორდინატები და დრო K და K’ ათვლის ინერციულ სისტემებში, ხოლო  v არის მათი ფარდობითი მოძრაობის სიჩქარე.

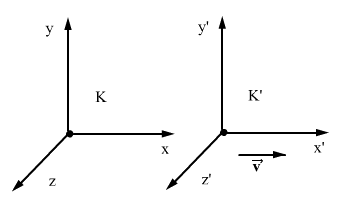
ამასთან არ გვაქვს არავითარი საფუძველი, ვიფიქროთ, რომ დრო K’ სისტემაში ემთხვევა დროს K სისტემაში, როგორც ეს უსიტყვოდ იგულისხმებოდა კლასიკურ ფიზიკაში. სიმარტივისთვის სიჩქარის მიმართულება ავარჩიოთ х და х’ ღერძების თანხვედრად. ვთქვათ  t’ დროის მომენტში   х’, у’, z’ კოორდინატების მქონე წერტილში ხდება რაღაც ფიზიკური პროცესი, რასაც დავარქვათ ხდომილება. ჩვენს ამოცანას წარმოადგენს  K’ სისტემაში მომხდარი ხდომილების კოორდინატებისა და დროის х, y, z, t განსაზღვრა K სისტემაში.

ათვლის საწყისად ავარჩიოთ t=0 მომენტი, როცა  K’ სისტემის სათავე ემთხვეოდა K სისტემის სათავეს. ვთქვათ t=0 მომენტში კოორდინატთა სათავიდან დაიწყო გავრცელება სფერულმა ელექტრომაგნიტურმა ტალღამ. K სისტემაში ტალღური ზედაპირის განტოლებას აქვს სახე

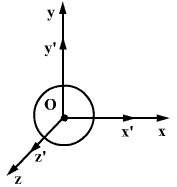
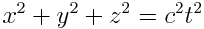
ანუ

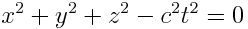(6.1)

რადგან, ეინშტეინის ფარდობითობის პრინციპის თანახმად, ელექტრომაგნიტური ტალღის გავრცელების კანონი და სიჩქარის სიდიდე ერთნაირია ყველა ინერციულ ათვლის სისტემაში, ამ განტოლებასთან ერთად სრულუფლებიანად შეგვიძლია დავწეროთ სფერული ტალღის განტოლება K’ სისტემაში

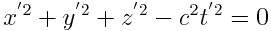
რადგან დროის საწყის მომენტში სისტემათა სათავეები ერთმანეთს ემთხვეოდა, ამიტომ

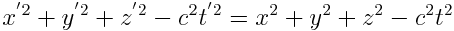(6.2)

კოორდინატებისა და დროის გარდაქმნის ფორმულები, პირველ რიგში, არ უნდა არღვევდნენ (6.1)და (6.2) თანაფარდობებს, ხოლო მეორე რიგში, უნდა იყოს წრფივი. წრფივობა გამომდინარეობს სივრცის ერთგვაროვნებისგან. რადგან K’ სისტემის მოძრაობა ხდება მხოლოდ х ღერძის გასწვრივ, ამიტომ у და z  კოორდინატების გარდაქნის ფორმულებს ექნება სახე

y'=y,   z'=z

х’ კოორდინატის х-ით გარდაქმნის კანონი შეიძლება ჩავწეროთ, გამომდინარე შემდეგი მოსაზრებიდან: თუ t=0 მომენტში  K და K’ სისტემების სათავეები ერთმანეთს ემთხვეოდა, მაშინ х’ სიბრტყის კოორდინატა K სისტემაში ჩაიწერება ასე х=νt. შესაბამისად, ყველაზე ზოგად შემთხვევაში შეიძლება დავწეროთ

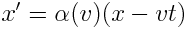(6.3)

სადაც კოეფიციენტი 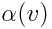 შეიძლება იყოს დამოკიდებული მხოლოდ ფარდობით სიჩქარეზე. ნუ გავაკეთებთ ნურავითარ დაშვებას ორ სისტემაში დროების დამთხვევაზე და შეგვიძლია წარმოვადგინოთ  t’ როგორც წრფივი ფუნქცია х-სა და t -სი.

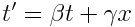(6.4)

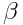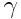ზოგადად   და  კოეფიციენტები შეიძლება იყოს დამოკიდებული v სიჩქარეზე. რომ აღმოჩენილიყო, რომ 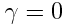, ხოლო 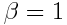, მაშინ ჩვენ დავუბრუნდებოდით გალილეის გარდაქმნებს. \(\alpha\),  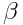და 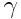 კოეფიციენტების განსაზღვრისთვის (6.3) და (6.4) უნდა ჩავსვათ (6.2)-ში. ეს გვაძლევს

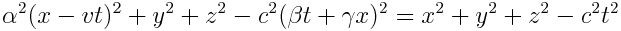
იგივეობის შესრულებისთის х²,t²და хt-ს შესაბამისი კოეფიციენტები ერთმანეთს გავუტოლოთ. ფრჩხილების გახსნით და შესაბამისი გარდაქმნების ჩატარებით მივიღებთ:

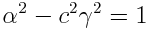
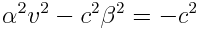
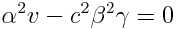
ამ სამი განტოლებიდან ვპოულობთ უცნობ სიდიდეებს \(\alpha\), 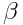  და  ,: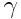

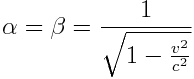
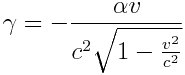
ამასთან ყველგან შევარჩიეთ ფესვების დადებითი ნიშნები. ჩავსვათ   \(\alpha\), 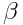  და 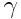 მნიშვნელობები  (6.3)-სა და(6.4)-ში და გვექნება:

,     ,     ,

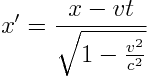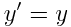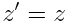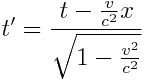(6.5)

ამ ფორმულებს ეწოდება ლორენცის გარდაქმნები. შტრიხიანიდან უშტრიხოზე პირუკუ გარდაქმნის ფორმულები ასეთია:

,    ,     ,

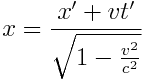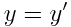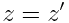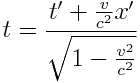(6.6)

ლორენცის გარდაქმნებს მივყევაღ დასკვნებამდე, რომლებიც ძირეულად უპირისპირდება სივრცესა და დროზე ჩვეულ შეხედულებებს.