ავარჩიოთ დეკარტის კოორდინატთა სისტემა ისე, რომ XY სიბრტყე ემთხვეოდეს M მატერიალური წერტილის მოძრაობის სიბრტყეს. ამოცანის ამოხსნისთვის გამოვიყენებთ კოორდინატთა ორ სისტემას – დეკარტის XOY კოორდინატთა სისტემას  i და j ორტებით და პოლარულს, რომლის ორტებია $e_{r}$ და $e_{\varphi}$.
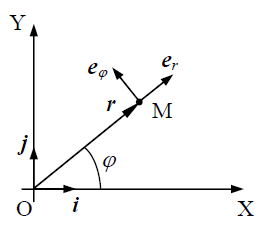
აღსანიშნავია, რომ მატერიალური წერტილის მოძრაობისას პოლარული სისტემის ორტები იცვლის ორიენტაციას, მაშინ როცა დეკარტის სისტემის ორტები არ იცვლის მიმართულებას.
პოლარულ სისტემაში მოცემული მატერიალური წერტილის მოძრაობის კანონი ჩავწეროთ დეკარტის კოორდინატთა სისტემაში:
                                (1)
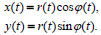
(1)-ის გაწარმოებით მივიღებთ:
                                 (2)
      (3)

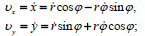
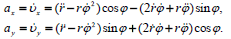
მეთოდი 1.

პოლარულ სისტემაში სიჩქარე და აჩქარება ჩაიწერება ასე:
(4)
(5)
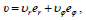
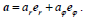
შესაბამისად, მატერიალური წერტილის სიჩქარისა და აჩქარების მდგენელები მიმართულებებზე, რომელიც მოცემულია არჩეული სისტემების ორტებით, დაკავშირებულია შემდეგი თანაფარდობებით:

      (6)
     (7)
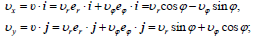
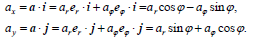
შევადაროთ გამოსახულებები (1) და (6), ასევე (2) და (7), მივიღებთ სიჩქარისა და აჩქარებიის სასურველ პროექციებს პოლარულ კოორდინატთა სისტემაში:

                         (8)

                  (9)

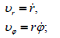
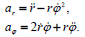
მეთოდი 2.

ჩავწეროთ მატერიალური წერტილის რადიუს-ვექტორი პოლარულ კოორდინატებში:
                           . (10)
რადგან მატერიალური წერტილის მოძრაობისას პოლარული სისტემის ორტების $e_{r}$-სა და $e_{\varphi}$-ის ორიენტაციის ცვლილება ხდება, ამიტომ ვიპოვნოთ მათი ცვლილების სიჩქარე

                        (11)

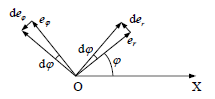
ახლა იმავე კოორდინატთა სისტემაში წერტილის სიჩქარისა და აჩქარების მოსაძებნად საჭიროა რადიუს-ვექტორი (10) გავაწარმოოთ დროით (11)-ის გათვალისწინებით.

                    (12)
(13)
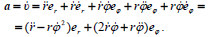
(12) და (13)-ის შესაბამისად მატერიალური წერტილის სიჩქარისა და აჩქარების საძებნი მდგენელები პოლარულ კოორდინატებში იქნება
(14)
(15)
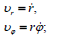
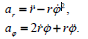
როგორც ვხედავთ ამოხსნის ორივე მეთოდი ერთდაიგივე შედეგს გვაძლევს.