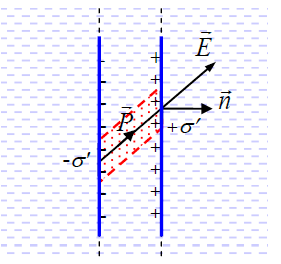
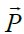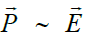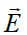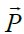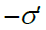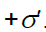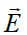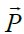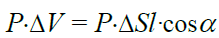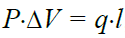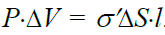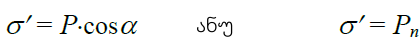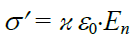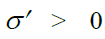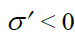მოცემული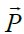 
პოლარიზაციის ვექტორით შეიძლება განისაზღვროს პოლარიზაციული მუხტები და პირიქით. დიელექტრული გარემოს შიგნით აზრობრივად გამოვყოთ თხელი ფენა. ამ ფენის რაღაც ნაწილში ელექტრული ველის დაძაბულობა შეიძლება ჩავთვალოთ მუდმივად და, შესაბამისად, 
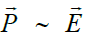. გამოვყოთ ასევე აზრობრივად თხელი პარალელეპიპედი (ან დახრილი ცილინდრი 
და ვექტორების გასწვრივ. მის ფუძეებზე ბმული მუხტები ხასიათდება სიმკვრივეებით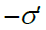 
და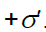 
. გავარკვიოთ, როგორ არიან ისინი დაკავშირებული 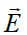-სა და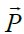-სთან. ცხადია, გამოყოფილი ელემენტის დიპოლური მომენტი ტოლია
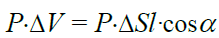(19.14)
მისი გამოთვლა ასევე შეიძლება ელემენტის ფსკერებზე მუხტის გამრავლებით ელემენტის სიგრძეზე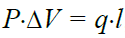 
, ანუ ამ სახით 
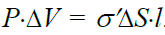. მაშინ ტოლობა (19.14) სახეს
. (19.14,ა)
აქედან გამომდინარეობს:
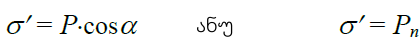. (19.15)
ამდენად ბმული მუხტების ზედაპირული სიმკვრივე პოლარიზაციის ვექტორის. ნორმალური მდგენელის ტოლია. პოლარიზაციისა და დაძაბულობის ვექტორების (19.9) ურთიერთკავშირის გათვალისწინებით, შეგვიძლია ასევე ჩავწეროთ:
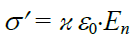(19.16)
იქ, სადაც En>0 (ანუ დაძაბულობის ძალწირები გამოდიან დიელექტრიკიდან)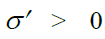 
. პირიქით, სადაც, En<0 (დაძაბულობის ძალწირები შედიან დიელექტრიკში) 
.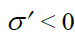