(განსაზღვრება) კონდენსატორი ეწოდება სისტემას. რომელიც შედგება ორი გამტარისაგან, რომელთა შორის, მათზე მოდულით ტოლი და ნიშნით საპირისპირო მუხტის მინიჭებისას, წარმოიქმნება გარე სხეულებისგან იზოლირებული ელექტრული ველი. აქ "იზოლირებულში" იგულისხმება მოთხოვნა, რომ დაძაბულობის ყველა ძალწირი იწყებოდეს ერთ გამტარზე და სრულდებოდეს მეორეზე დამოუკიდებლად იმისა, არის თუ არა კონდენსატორის სიახლოვეს დამუხტული ან დაუმუხტავი სხეულები. ასეთი პირობა შეიძლება განხორციელდეს მხოლოდ მაშინ, თუ გამტარები ერთმანეთთან ძალიან ახლოს (მათ ზომებთან შედარებით) არიან განლაგებულნი. ამ შემთხვევაში ველი პრაქტიკულად არ გამოდის გამტარების ფირფიტებს შორის მოთავსებული მცირე მიდამოდან. ამიტომ, მასზე არ მოქმედებს გარემოცვა - ველი არის იზოლირებული. რატომ არის ეს მნიშვნელოვანი ჩვენ ვნახავთ ოდნავ ქვევით. არსებობენ სხვადასხვა ტიპის კონდენსატორები. ბრტყელი კონდენსატორის დასახელებიდანაც ჩანს, რომ ის შედგება ორი ბრტყელპარალელური ლითონის ფირფიტისგან, რომლებიც გამოყოფილნი არიან ერთმანეთისგან დიელექტრიკით. არსებობენ სხვა ტიპის კონდენსატორებიც, მაგალითად, ცილინდრული, სფერული და ა.შ. მათთვის ასევე მნიშვნელოვანია გამტარის ფირფიტებს შორის მანძილის სიმცირე.

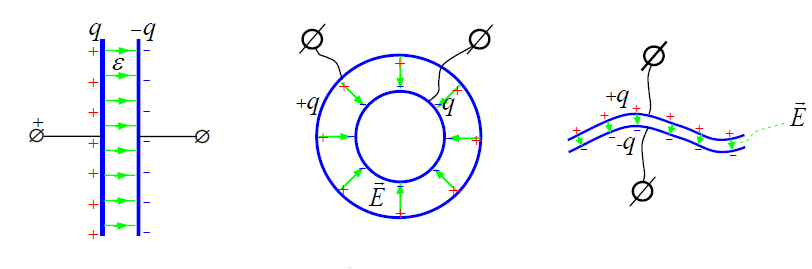
კონდენსატორები საჭიროა ელექტრული მუხტის, ელექტრული ენერგიისა და ელექტრული ველის დასაგროვებლად (კონდენსირებისთვის). ნებისმიერი ჭურჭლის უნარს დააგროვოს სითხე ახასიათებენ მისი ტევადობით. ანალოგიურად შემოდის "ელექტროტევადობის" ცნება. ელექტროტევადობა განისაზღვრება იმ მუხტის რაოდენობით, რაც უნდა მივაწოდოთ კონდენსატორის ფირფიტებს, რათა მათ შორის პოტენციალთა სხვაობა გახდეს ერთის ტოლი. (Si სისტემაში ეს არის 1ვოლტი).

(განსაზღვრება) კონდესატორის ელექტროტევადობა ეწოდება კონდენსატორის თითოეული ფირფიტის მუხტის მოდულის ფარდობას მათ შორის პოტენციალთა სხვაობაზე. ანალიზური ფორმით ეს ასე გამოიყურება:

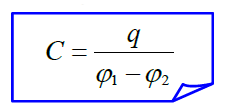                              (18.5)

აქ \(\varphi _{1}-\varphi _{2}\)  არის ფირფიტებს შორის პოტენციალთა სხვაობა, ამასთან დადებითი ფირფიტის პოტენციალს აკლდება უარყოფითი ფირფიტის პოტენციალი, ანუ ეს სხვაობა დადებითი სიდიდეა.  q  როგორც ზევით აღვნიშნეთ არის თითოეული ფირფიტის მუხტის მოდული.

ახლა გავარკვიოთ, რატომ არის მოცემული მახასიათებელი ცალსახად განსაზღვრებადი და რაში დაგვჭირდა ფირფიტებს შორის აღძრული ველის იზოლირებულობის მოთხოვნა. ამისთვის ჩავწეროთ, როგორ შეიძლება გამოვთვალოთ ფირფიტებს შორის პოტენციალთა სხვაობა მათზე მოდულით ტოლი და ნიშნით საპირისპირო მუხტების მინიჭების შემდეგ:

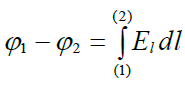
ეს სამართლიანია ნებისმიერი ელექტრული ველისა და ნებისმიერი ტრაექტორიისთვის, რომელიც იწყება კონდენსატორის ერთ ფირფიტაზე (1) და მთავრდება მეორეზე (2).

თუ ველი იზოლირებულია, მაშინ მასზე არ მოქმედებს კონდენსატორის გარემომცველი სხეულები და ის სრულად განისაზღვრება გეომეტრული ფაქტორებით (ფირფიტების ფორმებით, ზომებით და მათ შორის დაშორებით) და ფირფიტების მუხტით. უფრო მეტიც, შეიძლება ვამტკიცოთ, რომ ამ შემთხვევაში ველის ნებისმიერ წერტილში მისი დაძაბულობა პროპორციულია ფირფგიტებზე q მუხტისა. ანუ შეგვიძლია ვიგულისხმოთ ასეთი პროპორციულობა:

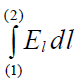 ~ ფირფიტებზე მუხტი (q).

მაგრამ ეს ხომ ნიშნავს, რომ მოცემული კონდენსატორის ფირფიტებს შორის პოტენციალთა სხვაობა მკაცრად პროპორციულია ფირფიტებზე გადაცემული მუხტისა. პროპორციულობის კოეფიციენტი კი სწორედ არის მისი ელეკტროტევადობის შექცეული სიდიდე:

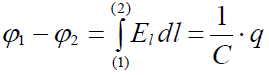                      (18.6)

აქედან კი გამომდინარეობს ზემოთ მოყვანილი განსაზღვრების 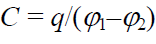 კორექტულობა (ცალსახობა).

რაზეა კონდენსატორის ელეკტროტევადობა დამოკიდებული? ახლახანს ჩატარებული ანალიზიდან ჩანს, რომ უპირველეს ყოვლისა დამოკიდებულია გეომეტრულ ფაქტორმებზე:
1. ფირფიტების ზომები;
2. ფირფიტების ფორმები;
3. მათ შორის დაშორება.
არის კიდევ ერთი მნიშვნელოვანი ფაქტორი, რომელიც მოქმედებს ელექტროტევადობაზე:
4. ფირფიტებს შორის მოთავსებული იზოლატორის დიელექტრული შეღწევადობა – \(\varepsilon\).
ჯერჯერობით ეს სიდიდე შემოვიღოთ ფორმალურად. ჩავთავალოთ, რომ ის ტოლია დიელექტრიკით შევსებული კონდენსატორის ელეკტროტევადობის ფარდობისა შეუვსებელი კონდენსატორის ელეკტროტევადობასთან:

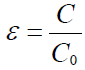                    (18.7)

შეიძლება თუ არა გავთვალოთ კონდენსატორის ელექტროტევადობა, ვიცით რა მისი გეომეტრია და \(\varepsilon\) ? ანალიზური სახით შედეგი შეიძლება მიიღწეს მხოლოდ ზოგიერთ უმარტივეს (თუმცა ყველაზე მნიშვნელოვან) შემთხვევაში, რომლებიც განსაზღვრული სიმეტრიებით ხასიათდება - ბრტყელი, ცილინდრული და სფერული კონდენსატორებისთვის. ვნახოთ როგორია თითოეულ ამ შემთხვევაში ელექტროტევადობის გათვლის პროცედურა.

• 1. უპირველეს ყოვლისა, უნდა განვსაზღვროთ 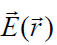 ველის დაძაბულობა ფირფიტებს შორის სივცეში. რადგან საუბარი არის მხოლოდ ზემოთ ჩამოთვლილ სიმეტრიულ შემთხვევებზე, მოსახერხებელია გამოვიყენოთ გაუსის თეორემა.
• 2. ფირფიტებს შორის პოტენციალთა სხვაობა ახლა შეიძლება ვიპოვნოთ 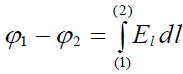 გამოსახულების გამოყენებით და ერთი ფირფიტიდან მეორეზე ძალწირების გასწვრივ უმარტივესი ტრაექტორიის შერჩევით. როგორც უკვე ვიცით შედეგი აუცილებლად იქნება ფირფიტის q მუხტის პროპორციული სიდიდე.
• 3. ელექტროტევადობის განსაზღვრების გამოყენებით ფირფიტის მუხტის მოდული გავყოთ ფირფიტებს შორის პოტენციალთა სხვაობაზე.  

მაგალითი. ვაჩვენოთ, როგორ შეიძლება პრაქტიკაში გამოვიყენოთ ის ნაბიჯები, რომლებიც ზევით მოვიყვანეთ კონდენსატორის ელექტროტევადობის გასათვლელად მოვიყვანეთ.

​1. ბრტყელი კონდენსატორი. ერთი შეხედვით გაუსის თეორემა არ გამოდგება ფირფიტებს შორის ველის დაძაბულობის განსასაზღვრად, რადგან ნათელია, რომ ასეთ სისტემაში ველი მნიშვნელოვნად ასიმეტრულია თითოეული დამუხტული ფირფიტის მიმართ. გაუსის თეორემაზე საუბრისას მოთხოვნილი პირობებების დამაკმაყოფილებელი ზედაპიორის შერჩევა შეუძლებელი გამოდის. თუ დროებით მოვაცილებთ ერთერთ ფირფიტას, ხოლო დარჩენილს ჩავთვლით უსასრულო სიბრტყედ (პრაქტიკაში თხელი დიდი ზომების ფირფიტა), მაშინ ყველაფერი იცვლება. ამ შემთხვევაში გაუსის თეორემის გამოყენების პროცედურა  წარმოვადგინოთ "შემოკლებული სქემით".

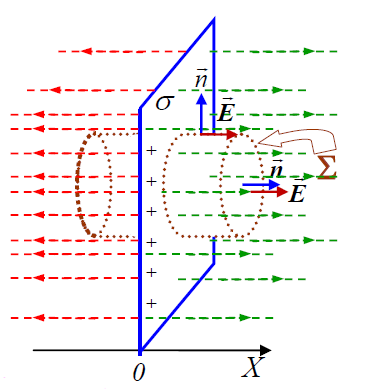
დავიწყოთ ნახაზით. ჩვენს მიერ შერჩეულ სწორი წრიული ცილინდრის ჩაკეტილ ზედაპირში დაძაბულობის ვექტორის ნაკადი ტოლია:

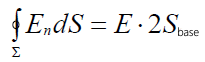
ამ ზედაპირის შიგნით მოქცეული მუხტი ტოლია \(\sigma S_{base}\).  გაუსის თეორემის თანახმა გვექნება:

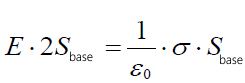
და აქედან მივიღებთ ველის დაძაბულობას:

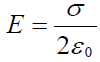                       (18.8)
როგორც ვხედავთ, დაძაბულობა არ არის დამოკიდებული x კოორდინატზე - დამუხტული სიბრტყიდან მანძილზე, ანუ ეს ველი არის ერთგვაროვანი. რა თქმა უნდა, ეს შეესატყვისება მხოლოდ ჰიპოთეტურ შემთხვევას "უსასრულო დამუხტულ სიბრტყეს". სინამდვილეში ასეთი უსასრულო მუხტები არ არსებობს - პრაქტიკულად ეს ნიშნავს, რომ ჩვენს მიერ მიღებული შედეგი (18.8) სამართლიანი იქნება სიბრტყიდან ნცირე დაშორებებზე ფირფიტის კიდეებიდან კი შორს.

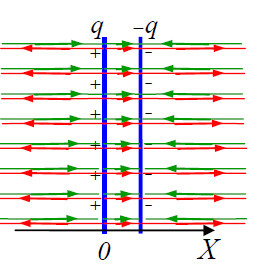
დავუბრუნდეთ ბრტყელი კონდენსატორის ფირფიტებს შორის ველის საკითხს. აღმოჩნდა რომ ამ ველის მოძებნა სულაც არ არის ახლა ძნელი მოსაძებნი სუპერპოზიციის პრინცციპის გამოყენებით. წარმოვადგინოთ მისი გამოყენება ამ ნახაზზე. თითოეული ფირფიტის მიერ შექმნილი ველების ძალწირები დავხაზოთ განსხვავებული ფერებით. მოჩანს, რომ ფირფიტებს შორის ძალწირები ერთნაირი მიმართულებისაა, ხოლო ფირფიტებს გარეთ საპირისპირო მიმართულებები აქვთ. რადგან ფირფიტების მუხტები მოდულებით ტოლია ამიტომ ტოლია მოდულებით მათ მიერ შექმნილი ველის დაძაბულობებიც. ეს ნიშნავს, რომ ფირფიტებს გარეთ ველები ერთმანეთს აქრობენ და შედეგობრივი ველის დაძაბულობა არის ნული. და პირიქით, ფირფიტებს შორის სივრცეში ველების მიმართულება ერთმანეთს ემთხვევა და შედეგობრივი დაძაბულობა გამოდის ორჯერ მეტი ვიდრე ერთი ფირფიტის ველის დაძაბულობა იქნებოდა.  ჩავწეროთ გამოსახულება დაძაბულობის მოდულისთვის:

(18.9)

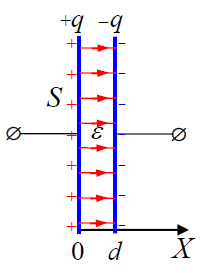
2. ბრტყელ კონდენსატორში ფირფიტებს შორის პოტენციალთა სხვაობის მოსაძებნად ავარჩიოთ ტრაექტორია ნებისმიერი ძალწირის გასწვრივ, ანუ შეიძლება ОХ ღერძის გასწვრივაც. მივიღებთ:

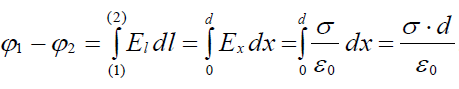
3. ახლა დაგვრჩა მხოლოდ გამოვიყენოთ კონდენსატორის ელექტროტევადობის განსაზღვრება და ფირფიტების მუხტებსა, მათ ზედაპიროს ფართობსა და ზედაპირული მუხტის სიმკვრივესს შორის ცხადი თანაფარდობით :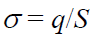

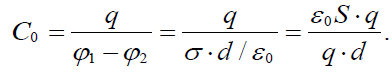
q-ზე შეკვეცით მივიღებთ ჰაერის (დიელექტრიკის გარეშე) კონდენსატორის ელექტროტევადობას. გავითვალისწინოთ, რომ ერთგვაროვანი დიელეტრიკით შევსებული კონდენსატორის ელექტროტევადობა, როგორც ეს გამომდინარეობს (18.7) გამოსახულებიდან, უდრის ჰაეროვანი კონდესატორის ელექტროვადობა გამრავლებული დიელექტრიკულ შეღწევადობაზე. საბოლოოდ ვღებულობთ ბრტყელი კონდენსატორის ელექტროტევადობის ფორმულას:

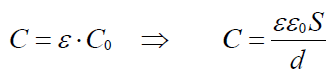                            (18.10)
სადაც S არის კონდენსატორის ფირფიტის ფართობი, ხოლო d – ფირფიტებს შორის მანძილი.