 |
მცირე პლანეტა, ერთ-ერთი უდიდესი (საშუალო დიამეტრი 525 კმ, მასა 2,6*1020კგ) ასტეროიდ ვესტას ბრუნვა გადაღებული კოსმოსური ხომალდიდან. ვესტას ბრუნვის პერიოდია 5.342 საათი. |
მყარი სხეულის ბრუნვის კინემატიკის აღსაწერად მოსახერხებელია კუთხური სიდიდეები: კუთხური გადაადგილება \(\Delta \varphi\), კუთხური სიჩქარე \(\omega\).
\(\omega =\frac{\Delta \varphi }{\Delta t}; (\Delta t\rightarrow 0)\),
და კუთხური აჩქარება \(\varepsilon \);
\(\varepsilon =\frac{\Delta\omega }{\Delta t}; (\Delta t \rightarrow 0).\)
ამ ფორმულებში კუთხე გამოისახება რადიანებით. მყარი სხეულების ბრუნვისას უძრავი ღერძის გარშემო, მის მიმართ სხეულის ყველა წერტილი მოძრაობს ერთნაირი კუთხური სიჩქარითა და ერთნაირი კუთხური აჩქარებით. ბრუნვის დადებით მიმართულებად მიჩნეულია საათის ისრის მოძრაობის საწინააღმდეგო მიმართულება.

ნახ.1. დისკოს ბრუნვა O წერტილში მართობულად გამავალი ღერძის მიმართ
\(\Delta m\) მასის სხეულის მცირე გადაადგილებისას კუთხური გადაადგილების \(\Delta \varphi \) და \(\Delta \vec{s}\) წრფივი გადაადგილების ვექტორის მოდულს შორის კავშირი გამოისახება შემდეგნაირად:
\(\Delta \vec{s}=r\Delta \varphi \),
სადაც \(r\) -\(\vec{r}\) რადიუსის ვექტორის მოდულია (ნახ.1). აქედან გამომდინარეობს კავშირი წრფივი და კუთხური სიჩქარეების მოდულებს შორის:
\(v=\omega r\),
და კავშირი წრფივი და კუთხური აჩქარებების მოდულებს შორის:
\(a=a\iota =r\varepsilon \).
ვექტორები \(\vec{v}\) და \(\vec{a}=\vec{a}_{\iota }\) მიმართულია \(r\) რადიუსიანი წრეწირის გასწვრივ. გავიხსენოთ ასევე მრუდწირული მოძრაობისას აღიძვრება ცენტრისკენული აჩქარებაც, რომლის მოდული ტოლია:
\(a_{n}=\frac{v^{2}}{r}=\omega ^{2}r\).
მბრუნავი სხეული დავანაწილოთ მცირე \(\Delta m_{i}\) მასის ნაწილებად, ბრუნვის ღერძამდე მანძილი ავღნიშნოთ \(r_{i}\)- თი, ხოლო წრფივი სიჩქარის მოდული ავღნიშნოთ \(v_{i}\)-თი. მაშინ მრუნავი სხეულის კინეტიკური ენერგია შეიძლება დავწეროთ შემდეგნაირად:
\(E_{k}=\sum_{i}\frac{\Delta mv_{i}^{2}}{2}=\sum_{i}\frac{\Delta m(r_{i}\omega )^{2}}{2}=\frac{\omega ^{2}}{2}\sum_{i}\Delta m_{i}r_{i}^{2}\)
ფიზიკურ სიდიდე \(\sum_{i}\Delta m_{i}r_{i}^{2}\) -ს ეწოდება სხეულის ინერციის მომენტი და აღინიშნება \(I\)-თი:
\(I=\sum_{i}\Delta m_{i}r_{i}^{2}\)
\(\Delta m \to 0\) ზღვარში ეს ჯამი გადადის ინტეგრალში. ინერციის მომენტის ერთეული \(Si\)–ში არის კილოგრამი მეტრ კვადრატი (კგ*მ2). ამგვარად, უძრავი ღერძის მიმართ მბრუნავი სხეულის კინეტიკური ენერგია შეიძლება წარმოვადგინოთ შემდეგი სახით:
\(E_{k}=\frac{I\omega ^{2}}{2}\)
ეს ფორმულა ძალიან გავს წრიფავად მოძრავი სხეულის კინეტიკური ენერგიის გამოსათვლელ ფორმულას \(\frac{mv^{2}}{2}\), უბრალოდ აქ მასის მაგივრად ინერციის მომენტია და წრიფივი სიჩქარის მაგივრად კუთხური სიჩქარე.
ბრუნვითი მოძრაობის დინამიკაში ინერციის მომენტი იგივე როლს ასრულებს, რასაც მასა მოძრავი სხეულის დინამიკაში. მაგრამ არსებობს პრინციპული განსხვავება: თუ მასა დამოკიდებული არ არის სხეულის მოძრაობაზე, ინერციის მომენტი დამოკიდებულია იმაზე, თუ რომელი ღერძის გარშემო ბრუნავს სხეული. სხვადასხვა ბრუნვის ღერძებისადმი ერთიდაიგივე სხეულების ინერციის მომენტები განსხვავებულია. ბევრ ამოცანაში განიხილება შემთხვევა, როდესაც მყარი სხეულის ბრუნვის ღერძი გადის ამ სხეულის მასათა ცენტრში. ისეთი სისტემის მასათა ცენტრი, რომელიც შედგება \(m_{1}\) და \(m_{2}\) მასებისგან. რომელთაგან თითოეულის კოორდინატებია \(x_{1}\), \(y_{1}\) და \(x_{2}\), \(y_{2}\) (ნახ.2), განისაზღვრება ფორმულებით:
\(x_{c}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}\); \(y_{c}=\frac{m_{1}y_{1}+m_{2}y_{2}}{m_{1}+m_{2}}\).
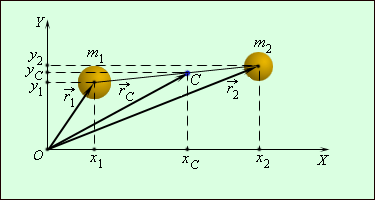
(ნახ.2) ორი ნაწილისაგან შემდგარი სისტემის მასათა ცენტრი.
ვექტორულ ფორმაში ეს გამოსახულებები მიიღებს შემდეგ სახეს:
\(r_{c}=\frac{m_{1}\vec{r}_{1}+m_{2}\vec{r}_{2}}{m_{1}+m_{2}}\)
ანალოგიურად ბევრი ნაწილაკებისგან შემდგარი სისტემისთვის მასათა ცენტრის რადიუს ვექტორი\(\vec{r}_{c}\) განისაღვრება შემდეგი გამოსახულებით:
\(\vec{r}_{c}=\frac{\sum m_{i}\vec{r_{i}}}{\sum m_{i}}\)
რთული ფორმის სხეულის მასათა ცენტრის გამოსათვლელად \(\vec{r}_{c}\) ფორმულა იცვლება ინტეგრალებით. ადვილი დასანახია, რომ ერთგვაროვანი სიმძიმის ველის მოქმედებისას სხეულის მასათა ცენტრი შეესაბამება სხეულის სიმძიმის ცენტრს. ამოტომ რთული ფორმის სხეულის მასათა ცენტრის განსაზღვრა შეიძლება შემდეგი გზით: მიმდევრობით დავკიდოთ სხეული სხვადასხვა ადგილით და გავატაროთ საკიდის მართობული წრფეები.(სურ.3)
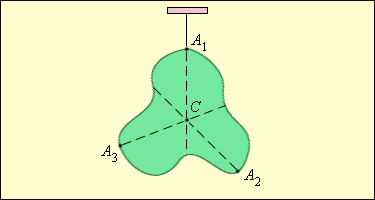
(სურ. 3) რთული ფორმის სხეულის მასათა ცენტრის განსაზღვრა A1, A2, A3 წერტილებზე ჩამოკიდებით.
თუ სხეული ჩამოკიდებულია მასათა ცენტრით მაშინ იგი იმყოფება განურჩეველ წონასწორობაში. ნებისმიერი მოძრაობა შეიძლება დავშალოთ ორ მოძრაობად: მასათა ცენტრის სიჩქარით გადატანით მოძრაობად და ბრუნვად მასათა ცენტრზე გამავალი ღერძის მიმართ. მაგალითად შეიძლება გამოდგეს ბორბალი, რომელიც ბრუნავს სრიალის გარეშე. ბორბლის ბრუნვისას მისი ყველა წერტილი ბრუნავს ნახატის სიბრტყის პარალელულ სიბრტყეში.
ასეთ მოძრაობას სიბტყული მოძრაობა ეწოდება. სიბრტყული მოძრაობისას მყარი სხეულის კინეტიკური ენერგია ტოლია გადატანითი მოძრაობის კინეტიკური ენერგიისა და სხეულის ბრუნვის კინტიკური ენერგიის ჯამის, რომელიც ბრუნავს იმ ღერძის მიმართ რომელიც გადის ამ სხეულის მასათა ცენტრზე და მართობულია იმ სიბრტყისა, რომელშიც მოძრაობს ამ სხეულის წერტილები:
\(E_{k}=\frac{mv_{c}^{2}}{2}+\frac{I_{c}\omega ^{2}}{2}\)
სადაც \(m\)– მთელი სხეულის მასაა, ხოლო IC– სხეულის ინერციის მომენტია, მის მასათა ცენტრზე გამავალი ღერძის მიმართ.
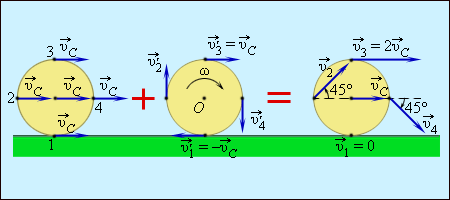
სურ. 4. ბორბლის ბრუნვა როგორც გადატანითი მოძრაობისა \(\vec{v}_{c}{tex} áá {tex}\omega =\frac{v_{c}}{R}\) კუთხური სიჩქარით მოძრაობის ჯამი.
მექნიკაში მტკიცდება შემდეგი თეორემა მასათა ცენტრის მოძრაობის შესახებ: სხეულის ან ურთიერთმოქმედ სხეულთა სისტემის მასათა ცენტრზე გარე ძალის მოქმედებისას, მასათა ცენტრი მოძრაობს როგორც მატერიალური წერტილი, რომელშიც განაწილებულია მთელი სხეულის მასა. ამ პროცესს კარგად ასახავს ქვემოთ მოცემული სურათი (სურ. 5) სურათზე გამოსახულია სხეულის მოძრაობა, რომელზეც მოქმედებს სიმძიმის ძალა. სხეულის მასათა ცენტრი მოძრაობს პარაბოლაზე, როგორც მატერიალური წერტილი, მაშინ როცა ყველა დანარჩენი წერტილი უფრო რთულ ტრაექტორიებზე მოძრაობენ.
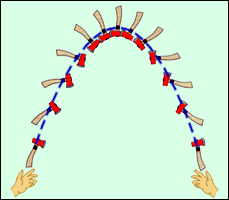
(სურ. 5) მყარი სხეულის მოძრაობა სიმძიმის ძალის მოქმედების ქვეშ.
თუ მყარი სხეული ბრუნავს რომელიმე უძრავი ღერძის მიმართ, მაშინ მისი ინერციის მომენტი \(I\) შეიძლება გამოისახოს ამ სხეულის \(I_{c}\) ინერციის მომენტით მის მასათა ცენტრზე გამავალი ღერძის მიმართ, რომელიც პარალელურია პირველი ღერძისა.

სურ. 6. ბრუნვის ღერძის პარალელურად გადატანის შესახებ თეორემის დამტკიცება.
განვიხილოთ ნებისმიერი ფორმის მყარი სხეული (სურ. 6). \(XOY\) კოორდინატთა სისტემის სათავედ ავირჩიოთ \(O\) წერტილი, რომელიც ემთხვევა სხეულის მასათა \(C\) ცენტრს. დავუშვათ ერთ-ერთი ბრუნვის ღერძი გადის მასათა ცენტრში ხოლო მეორე– ნებისმიერ \(P\) წერტილში რიმელიც \(C\)–სგან \(d\) მანძილითაა დაშორებული. ორივე ღერძი ნახაზის პერპენდიკულარულია. დავუშვათ \(\Delta m_{i}\)–მყარი სხეულის მასის რაღაც მცირე ელემენტია. ინერციის მომენტის განსაზრვრების თანახმად:
\(I_{c}=\sum \Delta m_{i}(x_{1}^{2}+y_{1}^{2})\),
\(I_{P}=\sum \Delta m_{i}\left | (x_{i}-a)^{2}+(y_{i}-b)^{2} \right |\)
გამოსახულება\(I_{P}\)–სთვის შეიძლება გარდავქმნათ შემდეგნაირად:
\(I_{P}=\sum \Delta m_{i}(x_{1}^{2}+y_{1}^{2})+\sum \Delta m_{i}(a^{2}-b^{2})-2a\sum \Delta m_{i}x_{i}-2b\sum \Delta m_{i}y_{i}\)
რადგან კოორდინატთა სათავე ემთხვევა მასათა ცენტრს, ბოლო ორი წევრი 0 ის ტოლი გამოდის. ეს გამომდიმარეობს მასათა ცენტრის განსაზღვრიდან. საყურადღებოა, რომ
\(I_{P}=I_{C}+md_{2}\),
სადაც m – მთლიანი სხეულის მასაა. ამ შედეგს ეწოდება შტაინერის თეორემა (თეორემა ბრუნვის ღერძის პარალელური გადატანის შესახებ).
ნიუტონის მეორე კანონი შეიძლება განვაზოგადოთ მყარი სხეულის ბრუნვაზე უძრავი ღერძის მიმართ. სურ. 8– ზე გამოსახულია რომელიღაც მყარი სხეული, რომელიც ბრუნავს \(O\) წერტილზე გამავალ ნახატის პერპენდიკულარულ ღერძის მიმართ. გამოვყოთ ნებისმიერი მცირე ელემენტი \(\Delta m_{i}\) მასით. მასზე მოქმედებს შიგა და გარე ძალები. ყველა ძალის ტოლქმედია \(\vec{F}_{i}\) ის შეიძლება დავშალოთ ორ მაბრუნებელ \(\vec{F}_{i\tau }\) და რადიანულ \(\vec{F}_{ir}\) მდგენელად. რადიანული მდგენელი \(\vec{F}_{ir}\) ქმნის ცენტისკენულ აჩქარება \(a_{n}\)–ს.
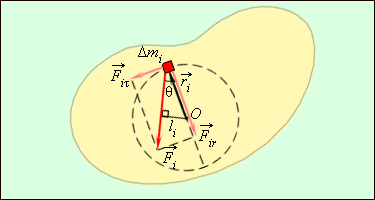
(სურ. 7) მაბრუნებელი \(\vec{F}_{i\tau }\) და რადიანული \(\vec{F}_{ir}\) ,რომლებიც მოქმედებენ ელემენტ \(\Delta m_{i}\)–ზე და ადგენს ძალა \(\vec{F}_{i}\)–ს.
\(\vec{F}_{i\tau }\) მდგენელი იწვევს \(\Delta m_{i}\) მასის ტანგენციალურ \(\vec{a}_{i\tau }\) აჩქარებას. ნიუტონის მეორე კანონს სკალარულ ფორმაში ექნება შემდეგი სახე:
\(\Delta m_{i}a_{i\tau}=F_{i\tau}=F_{i}\sin \theta\), ან \(\Delta m_{i}r_{i}\varepsilon=F_{i}\sin \theta\)
სადაც \(\varepsilon =\frac{a_{i\tau}}{r_{i}}\)– მთელი სხეულის კუთხური აჩქარებაა. თუ განტოლების ორივე მხარეს გავამრავლებთ \(r_{i}\) –ზე, მივიღებთ:
\(\Delta m_{i}r_{i}^{2}\varepsilon =F_{i}r_{i}\sin \theta =F_{i}l_{i}=M_{i}\)
სადაც \(l_{i}\)– \(\vec{F}_{i}\) ძალის მხარია, ხოლო \(M_{i}\) – ძალის მომენტი.
ეხლა საჭიროა იგივე შეთანხმებები დავწეროთ ყველა \(\Delta m_{i}\) ელემენტისთვის და შემდეგ ავჯამოთ მარჯვენა და მარცხენა მხარეები. ეს მოგვცემს:
\(\sum \Delta m_{i}r_{i}^{2}\varepsilon =\sum M_{i}\)
მარჯვენა მხარე სხვადასხვა წერტილზე მოქმედი ძალის მომენტების ჯამია, რომელიც შედგება ყველა გარე ძალის მომენტებისგან და ყველა შინაგანი ძალის მომენტების ჯამისგან.
\(\sum M_{i}=\sum (M_{i_{garegani}})+\sum (M_{i_{shinagani}})\)
მაგრამ ნიუტონის მეორე კანონის თანახმად ყველა შინაგანი ძალის მომენტების ჯამი 0–ის ტოლია, ამიტომ მარჯვენა მხარე დარჩება მხოლოდ გარე ძალების მომენტების ჯამი , რომელსაც ავღნიშნავთ \(M\)–ით. ანუ:
\(I\varepsilon =M\).
ეს კი მყარი სხეულის ბრუნვის დინამიკის მთავარი განტოლებაა. კუთხური აჩქარება \(\varepsilon\) და ძალის მომენტი \(M\), ამ ფორმულაში ალგებრული სიდიდეებია. ძირითადად სხეულის ბრუნვის დადებით მიმართულებად მიჩნეულია, საათის ისრის ბრუნვის საწინააღმდეგო მიმართულება.
გადატანითი მოძრაობის შესწავლის დროს შემოვიტანეთ ცნება სხეულის იმპულსის შესახებ \(\vec{p}\). ანალოგიურად სხეულის ბრუნვის დინამიკის შესწავლისას შემოგვაქვს იმპულსის მომენტი.
იმპულსის მომენტი ეწოდება ფიზიკურ სიდიდეს, რომელიც ტოლია სხეულის ინერციის მომენტის \(I\) და სხეულის ბრუნვის კუთხური სიჩქარის \(\omega\) ნამრავლის. იმპულსის მომენტი აღინიშნება \(L\) ასოთი და ტოლია:
\(L=I\omega\)
რმდენადაც \(\varepsilon =\frac{\Delta \omega }{\Delta t}; (\Delta tn \to 0),\) ბრუნვითი მოძრაობის განტოლება შეიძლება წარმოვადგინოთ შემდეგი სახით:
\(M=I\varepsilon =I\frac{\Delta \omega }{\Delta t}\) ან \(M\Delta t=I\Delta \omega =\Delta L.}\)
საბოლოოდ მივიღებთ:
\(M=\frac{\Delta L}{\Delta t}; (\Delta tn \to 0).\)
ეს განტოლება მიღებულია იმ შემთხვევისთვის თუ \(I=const\), მაგრამ სამრთლიანი ზოგადი შემთხვევისთვისაც, თუ ბრუნვის დროს სხეულის ინერციის მომენტი იცვლება.
თუ გარე ძალების ჯამური მომენტი \(M\) ნულის ტოლია, მაშინ იმპულსის მომენტი \(L=I\omega\) მოცემული ღერძის მიმართ ინახება:
\(\Delta L=0,\) თუ \(M=0\)
ესე იგი,
\(L=I\omega =const.\)
სწორედ ეს არის იმპულსის მუდმივობის კანონი. ამ კანონის საილუსტრაციოდ გამოდგება (სურ. 8), სადაც ასახულია ორი ერთ ღერძზე ჩამოცმული არადრეკადი მბრუნავი დისკოს დაჯახება.
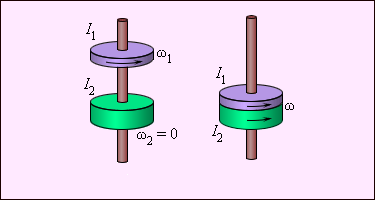
(სურ.8) ორი არადრეკადი დისკოს დაჯახება. იმპულსის მუდმივობის კანონი: \(I_{1}\omega_{1}=(I_{1}+I_{2})\omega\)
იმპულსის მუდმივობის კანონი სამართლიანი ნებისმიერი ჩაკეტილი სისტემისთვის. სხეულის ბრუნვის დინამიკის ძირითადი კანონი მოქმედებს თანაბრადაჩქარებული სხეულის მოძრაობის დროსაც. ამის მაგალითად შეიძლება გამოდგეს სხეულის (რკალის, ცილინდრის, ბურთის) გორვა დახრილ სიბრტყეზე. (სურ. 9)
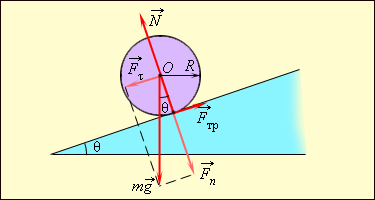
ნახ. 9
ბრუნვის ღერძი გადის სხეულის მასათა ცენტრში. ბრუნვის ღერძის მიმართ სიმძიმის ძალის \(m\vec{g}\) და რეაქციის ძალის \(\vec{N}\) მომენტები 0–ის ტოლია. მომენტს ქმნის მხოლოდ ხახუნის ძალა.
სხეულის ბრუნვის განტოლება:
\(I_{C}\varepsilon =I_{C}\frac{a}{R}=M=F_{\texttt{xax}}R,\)
სადაც \(\varepsilon\) – მბრუნავი სხეულის კუთხური აჩქარებაა, \(a\) – მისი ცენტრის წრფივი აჩქარება, ხოლო \(I_{C}\) – სხეულის ინერციის მომენტი მისი ცენტრის მიმართ.
ნიუტონის მეორე კანონი შემდეგნაირად ჩაიწერება:
\(ma=mg\sin \alpha -F_{\texttt{xax}}\)
დუ გამოვსახავთ ამ განტოლებებიდან \(F_{\texttt{xax}}\)–ს და გავუტოლებთ ერთმანეთს მივიღებთ:
\(a=\frac{mg\sin \theta }{(\frac{I_{C}}{R^{2}}+m)}.\)
მაგალითად ბურთისთვის \(I_{C}=\frac{2}{5}mR^{2},\) და ცილინდრისთვის \(I_{C}=\frac{1}{2}mR^{2},\) საყურადღებოა რომ ბურთი იგორებს ცილინდრზე სწრაფად.


