სხეულების ურთიერთქმედებისას ერთი სხეულის იმპულსი შეიძლება, ნაწილობრივ ან სრულად, გადაეცეს მეორე სხეულს. თუ სხეულიბის სისტემაზე სხვა სხეულიბის მხრიდან გარე ძალები არ მოქმედებენ, მაშინ ასეთ სისტემას ჩაკეტილი სისტემა ეწოდება.
ჩაკეტილ სისტემაში, მასში შემავალი ყველა სხეულის იმპულსების ვექტორული ჯამი, ამ სისტემის სხეულების ნებისმიერი ურთიერთქმედებისას, უცვლელი რჩება.
ბუნების ამ ფუნდამენტალურ კანონს იმპულსის მუდმივობის (შენახვის) კანონს უწოდებენ. ის ნიუტონის მეორე და მესამე კანონების შედეგს წარმოადგენს.
განვიხილოთ ჩაკეტილ სისტემაში შემავალი რაიმე ორი სხეული. ამ სხეულიბის ურთიერთქმედების ძალები აღვნიშნით \(\vec{F_{1}}\) და \(\vec{F_{2}}\) ნიუტონის მესამე კანონის თანახმად \(\vec{F_{2}}=-\vec{F_{1}}\) თუ ეს სხეულები \(t\) დროის განმავლობაში ურთიერთქმედებენ, მაშინ ურთიერთქმედების ძალების იმპულსები მოდულით ტოლია და საპირისპიროდაა მიმართული: \(\vec{F_{2}}t=-\vec{F_{1}}t.\) ამ სხეულიბის მიმართ გამოვიყენოთ ნიოტონის მეორე კანონი:
\(\vec{F_{1}}t=m_{1}\vec{v_{1}^{'}}-m_{2}\vec{v_1}; \vec{F_{2}}t=m_{1}\vec{v_{2}^{'}}-m_{2}\vec{v_{2}};\)
ეს ტოლობა ნიშნავს, რომ ორი სხეულის ურთიერთქმედების შედეგად მათი ჯამური იმპულსი არ იცვლება. ჩაკეტილ სისტემაში სხეულთა წყვილის ნებისმიერი სახის ურთიერთქმედების განხილვიდან შეიძლება გავაკეთოდ დასკვნა, რომ ჩაკეტილ სისტემის შინაგან ძალებს არ შეუძლიათ ჯამური იმპულსის, ე.ი. სისტემაში შემავალი ყველა სხეულის იმპულსების ვექტორული ჯამის შეცვალა.
ნახ. 1–ზე ორი სხვადასხვა მასის ბურთის, რომელთაგან ერთი დაჯახებამდე უძრავი იყო, არაცენტრალური შეჯახებისას იმპულსის შენახვის კანონია ნაჩვენები.
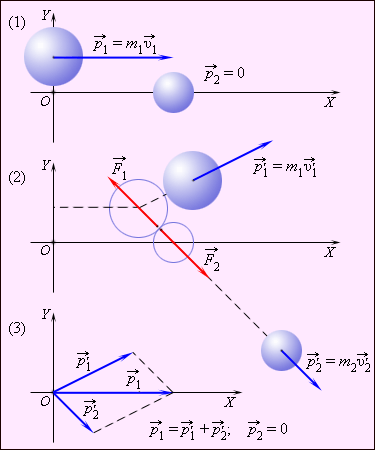
ნახ. 1.
სხვადასხვა მასის ბურთების არაცენტრალური შეჯახებისას.:1 – იმპულსები შეჯახებამდე; 2 - იმპულსები შეჯახების შემდეგ; 3 - იმპულსების დიაგრამა
ნახ. 1–ზე გამოსახილია ბურთების იმპულსის ვექტორები დაჯახებამდე და დაჯახების შემდეგ, დავაგეგმილოთ \(OX\) და \(OY\) ღერძებზე. იმპულსის შენახვის კანონი სამართლიანია ვექტორების ღერძებზე გეგმილებისთვისაც, კერძოდ, იმპულსების ამ დიაგრამიდან გამომდინარეობს, რომ დაჯახების შემდეგ ორივე ბურთის \(\vec{P_{1}^{'}}\) და \(\vec{P_{2}^{'}}\) იმპულსების ვექტორების გეგმილები %OY%ღერძზე მოდულით ტოლი უნდა იყოს და ჰქონდეთ სხვადასხვა ნიშანი, რომ მათი ჯამი ნულის ტოლი გამოვიდეს.
იმპულსის შენახვის კანონი ბევრ შემთხვევაში ურთიერთმოქმედი სხეულიბის სიჩქარეების პოვნის საშუალებას იძლევა, მაშინაც კი როცა მომქმედი ძალების სიდიდეები ცნობილი არ არის. ამის მაგალითად რეაქტიული მოძრაობა გამოდგება.
ქვემეხიდან გასროლის დროს ადგილი აქვს უკუგებას – ჭურვი მოძრაობს წინ, ქვემეხი კი უკან დაგორდება. ჭურვი და ქვემეხი – ურთიერთმოქმედი სხეულიბია. უკუგდებისას ქვემეხის მიერ მიღებული სიჩქარე დამოკიდებულია, მხოლოდ ჭურვის სიჩქარესა და მასების ფარდობაზე (ნახ. 2). თუ ქვემეხისა და ჭურვის სიჩქარეებს აღვნიშნავთ \(\vec{V}\) და \(\vec{v}\) ხოლო მასებს \(M\) და \(m\)–ით, მაშინ იმპულსის შენახვის კანონის საფუძველზე შეიძლება დაიწეროს \(OX\) ღერძზე გეგმილებისათვის
\(MV+mv=0; V=-\frac{m}{M}v.\)

ნახ.2.
უკუგება ქვემეხიდან გასროლისას

უკუგების პრინციპზეა დამყარებული რეაქტიული მოძრაობა. კოსმოსურ ხომალდში საწვავის წვისას, მაღალ ტემპერატურამდე გახურებული აირი დიდი \(\vec{u}\) სიჩქარეით გამოიტყორცნება ხომალდის კუდიდან. გამოტყორცნილი აირის მასა \(m\)–ით აღვნიშნოთ, ხოლო რაკეტის მასა აირის გამოსვლის შემდეგ \(M\)–ით. „ხომალდი–აირი“ ჩაკეტილი სისტემისათვის იმპულსის შენახვის კანონის საფუძველზე (ქვემეხიდან გასროლის ამოცანის ანალოგიურად) შეიძლება დაიწეროს:
\(V=-\frac{m}{M}u.\)
სადაც \(V\)– რაკეტის სიჩქარეა აირის გამოდინების შემდეგ. მოცემულ მომენტში იგულისხმება რომ, ხომალდის საწყისი სიჩქარე ნულის ტოლია my site.
ხომალდის სიჩქარისათვის მიღებული ფორმულა სამართლიანია მხოლოდ იმ სემთხვევაში, თუ დამწვარი (გადამუშავებული) აირი ხომალდიდან ერთდროულად გამოიტყოცვება. სინამდვილეში გამოდინება ხდება თანდათან, ხომალდის მთელი, აჩქარებული მოძრაობის პერიოდში. აირის ყოველი მომდევნო პორცია გამოიტყოცნება ხომალდიდან, რომელმაც უკვე შეიძინა რაღაც სიჩქარე.
ზუსტი ფორმულის მისაღებად აირის გამოდინების პროცესი უფრო დეტელურად უნდა იქნეს განხილული. ვთქვათ ხომალდს დროის \(t\) მომენტში \(M\) მასა აქვს და მოძრაობს \(\vec{v}\) სიჩქარით (ნახ. 3 (1)). დროის მცირე \(\Delta t\) ინტერვალში გამოედინება აირის რაღაც პორცია ფარდობითი სიჩქარით \(\vec{u}.\) ხომალდს \(t+\Delta t\) მომენტში ექნება სიჩქარე \(\vec{v}+\Delta \vec{v},\) ხოლო მასა გახდება ტოლი \(M+\Delta M\), სადაც \(\Delta M<0\) (ნახ. 3 (2)). ნათელია, რომ გამოტყორცნილი აირის მასა ტოლია \(-\Delta M>0\). აირის სიჩქარე \(OX\) ინერციულ სისტემაში იქნება ტოლი \(\vec{v}+\vec{u}.\) გამოვიყენოთ იმპულსის შენახვის კანონი. დროის \(t+\Delta t\) მომენტში ხომალდის იმპულსი ტოლია \((M+\Delta M)(\vec{v}+\Delta \vec{v}),\) ხოლო გამოტყორცნილი აირის იმპულსი კი \((-\Delta M)(\vec{v}+\vec{u}).\) დროის \(t\) მომენტში მთელი სისტემის იმპულსი ტოლია \(M\vec{v}.\) ვგულისხმობთ რა, რომ სისტემა „ხომალდი–აირი“ ჩაკეტილია შეიძლება დაიწეროს:
\(M\vec{v}=(M+\Delta M)(\vec{v}+\Delta \vec{v})-\Delta M(\vec{v}+\vec{u})\) ან \(M\Delta \vec{v}=\Delta M\vec{u}-\Delta M\Delta \vec{v}\)
\(\Delta M\Delta \vec{v}\) სიდიდის უგულვებესყოფა შეიძლება, რადგან \(|\Delta M|<<M\). ტოლობის ორივე მხარის \(\Delta t\)–ზე გაყოფით და \(\Delta t\rightarrow 0\) ზღვარზე გადასვლით, მივიღებთ
\(M\frac{\Delta \vec{v}}{\Delta t}=\frac{\Delta M}{\Delta t}\vec{u}\, \; (\Delta t\rightarrow 0)\) ან \(M\vec{a}=-\mu \vec{u}.\)

ნახ. 3.
ხომალდი მოძრაობს თავისუფალ სივრცეში (გრავიტაციის გარეშე). 1 – დროის \(t\) მომენტში. ხომალდის მასა \(M\), მისი სიჩქარე \(\vec{v}\).2 – ხომალდი\(t+\Delta t\) მომენტში. ხომალდის მასა \(M+\Delta M\), სადაც \(\Delta M<0\), მისი სიჩქარე \(\vec{v}+\Delta \vec{v},\) გამოტყორცნილი აირის მასა \(-\Delta M>0\), აირის ფარდიბითი სიჩქარე \(\vec{u},\) აირის სიჩქარე ინერციულ სისტემაში \(\vec{v}+\vec{u}\)

\(\mu =-\frac{\Delta M}{\Delta t}\; (\Delta t\rightarrow 0)\) სიდიდე საწვავის ხარჯია დროის ერთეულში. \(-\mu \vec{u}\) სიდიდეს წევის რეაქტიულ ძალას უწოდებენ – \(\vec{F_{p}}.\) წევის რეაქტიულ ძალა ხომალდზე აირის გამოდინების მხრიდან მოქმედებს, იგი მიმართულია ფარდობითი სიჩქარის საპირისპიროდ. დამოკიდებულება
\(M\vec{a}=\vec{F_{p}}=-\mu \vec{u},\)
გამოსახავს ნიუტონის მეორე კანონს ცვლადი მასის მქონე სხულისათვის. თუ აირი ხომალდის კუდიდან მკაცრად უკან გაიტყოცნება (ნახ. 3), მაშინ სკალარული სახით იგი ჩაიწერება:
\(Ma=\mu u\),
სადაც \(u\)– ფარდობითი სიჩქარის მოდულია. ამ ფორმულის ინტეგრირების საშუალებით შეიძლება ხომალდის საბოლოო \(v\) სიჩქარის გამოსათვლელი ფორმულის მიღება:
\(v=u\: \: ln\left (\frac{M_{0}}{M} \right )\)
სადაც \(\frac{M_{0}}{M}\) – ხომალდის საწყისი და საბოლოო სიჩქარეების ფარდობაა. ამ ფორმულის მიხედვით, შეიძლება ხომალდის სიჩქარე აღემატებოდეს აირის გამოდინების სიჩქარეს. აქედან გამომდინარეობს, რომ ხომალდს შეიძლება ჰქონდეს კოსმოსური ფრენისთვის აუცილებელი დიდი სიჩქარე. მაგრამ, ეს მიიღწევა საწვავის მნიშვნელოვანი რაოდენობის დანახარჯით, რაც ხომალდის მასის დიდ ნაწილს შეადგენს. მაგალითად, პირველი კოსმოსური სიჩქარის \(u=v_{1}=7,9\cdot 10^{3}\) მ/წმ მისაღწევად როცა \(u=3\cdot 10^{3}\) მ/წმ (აირის გამოდინების სიჩქარე საწვავის წვისას 2-4 კმ/წმ რიგისაა) ერთსაფეხურიანი ხომალდის სასტარტო მასა დაახლოებით 14–ჯერ უნდა აღემატებოდეს საბოლოო მასას. \(v=4u\) საბოლოო სიჩქარის მისაღწევად \(\frac{M_{0}}{M}\) ფარდობა უნდა იყოს 50–ის ტოლი.
სასტარტო მასის მნიშვნელოვანი შემცირება მიიღწევა მარვალსაფეხურიანი ხომალდის გამოყენებისას, როცა ხომალდს საფეხურები სცილდება საწვავის გამოლევის შემდეგ. შემდგომი გაქანების (სიჩქარის ზრდის) პროცესიდან გამოირიცხება საწვავის კონტეინერის მასა.


