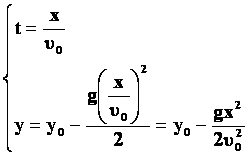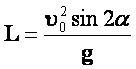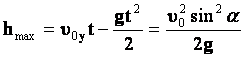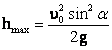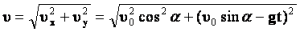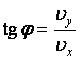1. ეს არის მოძრაობა სიბრტყეზე, ამიტომ მოძრაობის აღსაწერად აუცილებელია 2 კოორდინატი.
2. ვთვლით, რომ მოძრაობა მიმდინარეობს დედამიწის ზედაპირთან ახლოს, ამიტომ სხეულის აჩქარება არის თავისუფალი ვარდნის აჩქარება (a = g).

რადგან ჩვენ ვუგულებელყოფთ ჰაერის წინააღმდეგობას, ამიტომ აჩქარება მხოლოდ დედამიწისკენ არის მიმართული, (g) – მიმართულია (y) ვერტიკალური ღერძის გასწვრივ, ხოლო х ღერძის გასწვრივ მოძრაობა თაბარია და წრფივი.

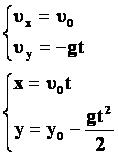
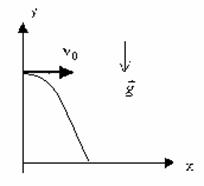
ჰორიზონტალურად გასროლილი სხეულის მოძრაობა

სიცქარის პროექციები და კოორდინატები გამოვსახოთ ვექტორების მოდულებით. 

იმისათვის რათა მივიღოტ ტრაექტორიის განტოლება, გამოვსახოთ დრო x კოორდინატის განტოლებიდან და ჩავსვათ y-ის განტოლებაში: 

- კოორდინატებს შორის კვადრატული დამოკიდებულებაა, ტრაექტორია პარაბოლაა!

ჰორიზონტისადმი კუთხით გასროლილი სხეულის მოძრაობა

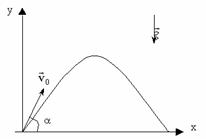
ამოცანის ამოხსნის ტანმიმდევრობა წინას ანალოგიურია.

ამოვხსნათ ამოცანა შემთხვევისტვის, როცა х₀=0 და y₀=0.

\(\left\{\begin{matrix} v_{x}=v_{0}\cos \alpha\\v_{y}=v_{0}\sin \alpha \end{matrix}\right.\)

\(\left\{\begin{matrix} x=v_{x}t=v_{0}t\cos \alpha\\y=v_{y}t-\frac{gt^{2}}{2}=v_{0}t\sin \alpha -\frac{gt^{2}}{2}\end{matrix}\right.\)

ვაჩვენოთ, რომ მოძრაობის ტრაექტორია ამ შემთხვევაშიც იქნება პარაბოლა. ამისთვის გამოვსახოთ Y კოორდინატა X-ით (მივიღებთ ტრაექტორიის განტოლებას):\(y=xtg\alpha -x^{2}\frac{g}{2v_{0}^{2}\cos ^{2}\alpha }\).

მივიღეთ კოორდინატებს შორის კვადრატული დამოკიდებულება. ე. ი. ტრაექტორია პარაბოლაა.

ვიპოვნოთ სხეულის ფრენის დრო დასაწყისიდან დაცემამდე. დაცემის წერტილში ვერტიკალური ღერძის კოორდინატა у=0. შესაბამისად, ამ ამოცანის ამოხსნისთვის უნდა ამოიხსნას განტოლება \(v_{0}t\sin \alpha -\frac{gt^{2}}{2}=0\) . მას ექნება ამოხსნა როცა t=0(მოძრაობის დასაწყისი) და \(t_{fl}=\frac{2v_{0}\sin \alpha }{g}\)

ფრენის დრო:

\(t_{fl}=\frac{2v_{0}\sin \alpha }{g}\)

გვეცოდინება რა ფრენის დრო, ვიპოვნით იმ მაქსიმალურ მანძილს, რომელიც გაიფრინა სხეულმა: \(L=v_{x}t_{fl}=\frac{v_{0}^{2}\sin 2\alpha }{g}\)

ფრენის სიშორე:

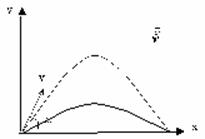
ამ ფორმულიდან გამომდინარეობს, რომ:

- ფრენის მაქსიმალური სიშორე მიიღწევა სხეულის ჰორიზონტისადმი 45⁰ კუთხით გასროლის შემთხვევაში;

- ერთნაირ მაძილზე შეიძლება სხეულის გადაგდება (ერთი და იგივე საწყისი სიჩქარეებით) ორნაირად – ე.წ.  ჩაკიდებული და დაფენილი ტრაექტორიები.

იმის გამოყენებით, რომ პარაბოლა სიმეტრიული ფიგურაა, ვიპოვნოთ მაქსიმალურ სიმაღლეს, რომელსაც აღწევს სხეული. დრო, რომელშიც სხეული აღწევს შუა გზას, ტოლია: \(t=\frac{v_{0}\sin \alpha }{g}\)

ასვლის დრო:

\(t=\frac{v_{0}\sin \alpha }{g}\)

მაშინ: 

მაქსიმალური სიმაღლე:

სხეულის სიჩქარე დროის ნებისმიერ მომენტში მიმართულია მოძრაობის ტრაექტორიის (პარაბოლის) მხების გასწვრივ და ტოლია 

კუთხე, რომლითაც მიმართულია სიჩქარის ვექტორი დროის ნებისმიერ მომენტში: