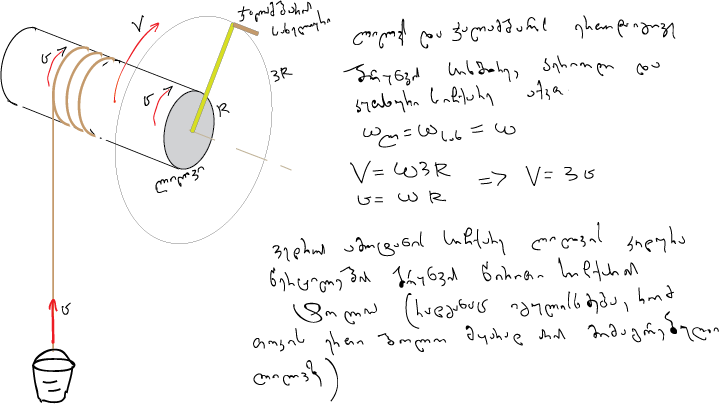
დიდი მადლობა წინა საკითხში ასე სიღრმისეულად რომ გამარკვიეთ. კიდევ მაქვს რამდენიმე შეკითხვა მრუდწირულ მოძრაობაზე 

1. როდესაც ჭის ჯალამბრის სახელურის რადიუსი 3-ჯერ მეტია ლილვის რადიუსზე და ვედრო 0.6 მ/წმ სიჩქარით ამოაქვთ, მაშინ რას უდრის სახელურის ბრუნვის წირითი სიჩქარე? ლილვი და ჯალამბარი ზუსტად რა არის, ვერ გავიგე. იქნებ ჭის სურათზე მაჩვენოთ. ამოცანის სწორი პასუხი 1,8 მ/წმ-ია. ე.ი. ვედროს სიჩქარე ლილვის რადიუსზეა დამოკიდებული? V_{ვედრო}=2пR_{ლილვი}n=0,6 მ/წმ და ჯალამბარი საჭის მსგავსია,  რასაც ჩვენ ვატრიალებთ, წყალი რომ ამოვიღოთ ჭიდან? მაშინ სახელურის ბრუნვის წირითი სიჩქარე იქნება V_{სახელური}=2пR_{სახელური}n=? ა.პ.თ რადგან R_{ლილვი}=R და R_{სახელური}=3R მაშინ V_{სახელური} / V_{ლილვი}=3 ე.ი სამჯერ მეტია და V_{სახელური}=1,8 მ/წმ. და სიხშირეები და პერიოდები ტოლი აქვთ ხომ? და რისი სიხშირე გამოდის, რა სიხშირით ამოგვაქვს წყლიანი ვედრო ჭიდან?

2. წავიკითხე, რომ სხვა სიჩქარეებისგან განსხვავებით წირითი სიჩქარე სკალარული სიდიდეა. თუმცა ტესტებში წირითი სიჩქარის მიმართულებას გვეკითხებოდნენ ბორბლის კონკრეტული წერტილისთვის და ეგ როგორ? 

3. როგორც ვიცი, კუთხური სიჩქარის ერთეულია რად/წმ. თუმცა ტესტებში კუთხური სიჩქარის ერთეულად წმ^-1 შემხვდა. ე.ი. თუ ф=2п შემობრუნების კუთხეს რადიანებში გამოვსახავთ, მაშინ კუთხური სიჩქარის ერთეული რად/წმ-ია. თუ ф-ს რიცხვით მნიშვნელობას (6,28) გავყოფთ დროზე, მაშინ წმ^-1 იგივე ჰერცი, ანუ კუთხურ სიჩქარესა და ბრუნვის სიხშირეს ერთნაირი ერთეული აქვთ. და კიდევ თუ შემობრუნების კუთხეს გრადუსებში გამოვსახავთ (360^o), კუთხური სიჩქარის ერთეული გრადუსი/წმ იქნება?

ბოდიში, ამდენი კითხვა ერთად რომ მოგაყარეთ, მაგრამ მიჭირს ფიზიკა, გამოცდები კი მიახლოვდება :(

1)  

2)    წირითი სიჩქარე სკალარული   სიდიდეა...  იგი მყისი სიჩქარის(წრეწირის მოცემულ წერტილში მხების გასწვრივ მიმართული ვექტორი) მოდულის ტოლია.

3)  დიახ!

ერთეულთა   SI  სისტემაში ბრუნვის სიხშირეს  და კუთხურ სიჩქარეს ერთიდაიგივე განზომილება  აქვთ ----- წმ^-1 = ჰც.... ...თუმც   ''ჰც''-ს   მაინც   უფრო  ხშირად   რხევების აღწერისას ხმარობენ......  ,,რად"-ს  კუთხური სიჩქარის შეფასებისას  უფრო დაზუსტების მიზნით ხმარობენ, ამიტომ იგი შეიძლება არც კი ჩაიწეროს(არც კი გამოითქვას)....

1 რად = (360/ \(\pi\))^o....  რხევების აღწერისას  \(\omega\) = 2\(\pi\)\(\nu\) (მსგავსად კუთხური სიჩქარისა)...

ამ დამოკიდებულების გამო  .\(\omega\) - ს ხშირად ციკლურ სიშირესაც უწოდებენ - რამეთუ ამ ფორმულიდან ჩანს , რომ იგი  გვიჩვენებს  2\(\pi\) წმ-ის განმავლობაში შესრულებულ რხევათა რიცხვს...  გამოდის რომ კუთხური სიჩქარე  2\(\pi\) წმ-ის განმავლობაში შესრულებულ ბრუნვათა რიცხვის  ტოლია.

კუთხური სიჩქარის არაძირითადი ერთეული ცხადია შეიძლება იყოს  (გრად/წმ)-ც...

---------------------------

_{ოლეგი გაბრიაძე}